Selection Sort – Algorithm, Implementation and Performance

The selection sort algorithm divides the array into two sub-arrays, namely the sorted sub-array and the unsorted sub-array. Initially, the sorted sub-array is empty, and the unsorted sub-array contains all the elements of the array. The algorithm then proceeds to find the minimum element from the unsorted sub-array and moves it to the sorted sub-array. This process is repeated until the entire array is sorted.

This Java tutorial will provide an in-depth exploration of selection sort, its working, its complexity, and its implementation in Java. Additionally, we will explore some of the key advantages and disadvantages of the selection sort.

1. How does Selection Sort Work?

During each iteration of the selection sort algorithm, the leftmost element of the unsorted sub-array is exchanged with the minimum element from the same sub-array. This results in the minimum element being moved to the beginning of the unsorted sub-array, which is now considered part of the sorted sub-array. The algorithm then moves on to the next iteration, using the remaining unsorted sub-array to repeat the process until the entire array is sorted.

Now, let’s understand the step-by-step working of the Selection sort Algorithm.

1. Assign the first index of the array as the starting index for the unsorted sub-array.
2. Find out the smallest element within the unsorted sub-array.
3. Swap the smallest element with the element located at the leftmost position within the unsorted sub-array.
4. Increment the starting index of the unsorted sub-array by 1.
5. Continue performing steps 2-4 until the entire array has been sorted.

After going through all the steps given above the array is finally sorted.

2. Selection Sort In Action

Now, let’s move on to an example and understand how it works.

Let us take an array [55, 29, 16, 23, 14].

1st Iteration:

To find the smallest value in the array, a linear traversal is performed from index 0 to 4. Currently, the 1st position holds 55, but upon searching the unsorted sub-array, you discover that the smallest value is 14.

Therefore, swap the values 14 and 55. The sorted sub-array will now have 14 at the 0th index. Now the array will look like this:

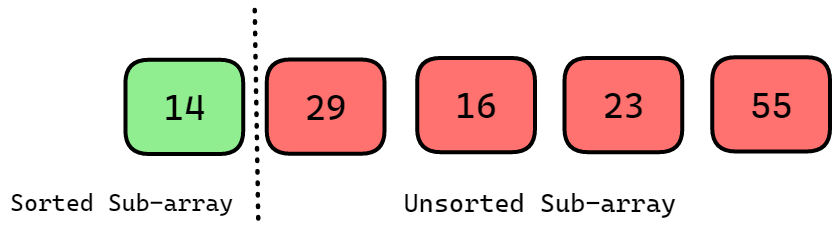
So now, 14 is placed at its correct position. Sub-array before the dotted vertical line represents the sorted sub-array and the sub-array after the dotted vertical line represents the unsorted sub-array.

2nd Iteration:

Repeat the linear traversal of the rest of the array for the 2nd position of the sorted sub-array. Currently, the 2nd position holds 29, but upon searching the unsorted sub-array, you discover that the smallest value is 16.

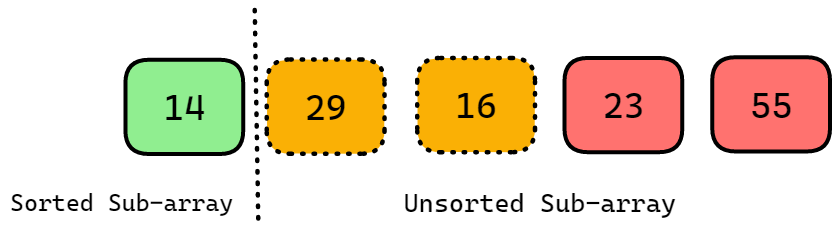
Therefore, swap the values 29 and 16. The sorted sub-array will now have 16 at the 1st index. Now array will look like this.

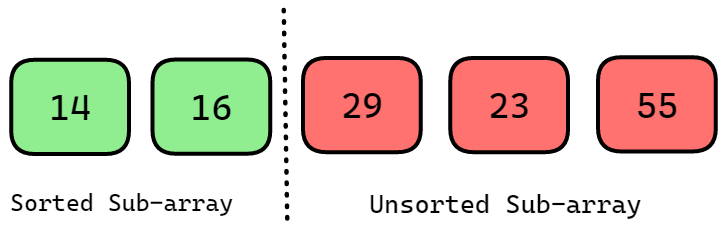
After two iterations, the program sorted and positioned the two smallest values at the beginning of the array.

3rd Iteration:

To obtain the 3rd position, which already has 29, continue traversing through the remaining elements of the array and identify the third smallest value in it. Now, 3rd smallest value is 23.

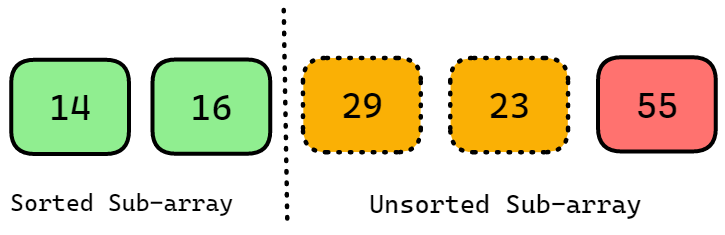
Therefore, swap the values 29 and 23. The sorted sub-array will now have 23 at the 2nd index. Now array will look like this.

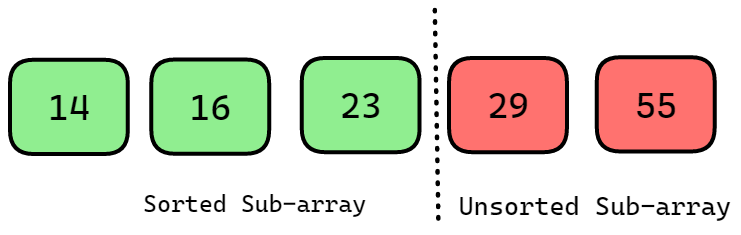
After three iterations, the program sorted and positioned the three smallest values at the beginning of the array.

4th Iteration:

Similarly, find 4rth smallest element for the sorted sub-array.

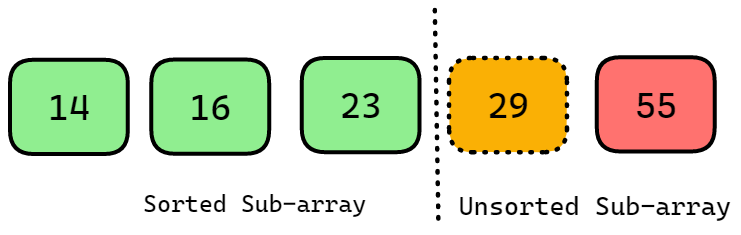
Now, 4rth smallest value is 29 itself which is already at its correct position so there is no need to swap any values. Now array will look like this.

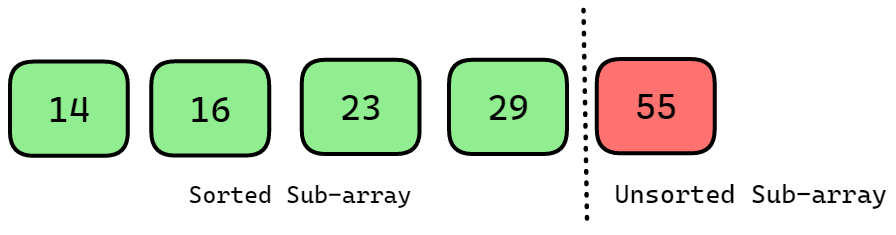
After four iterations, the program sorted and positioned the four smallest values at the beginning of the array. Now, the unsorted sub-array has only one value left, which indicates that it is already sorted, and no further iterations are necessary. The final sorted array looks like this.

3. Implementation of Selection Sort in Java

Let us hit the keyboard and write a program demonstrating how to implement selection sort in Java.

3.1. Sort

The selection_sort() function accepts an integer array “arr”. In this function, we have 2 loops, i.e one loop inside of another. The outer loop keeps track of the iterations and it starts from the first element and goes up to the second-to-last element in the array. The inner loop then iterates through the remaining unsorted portion of the array and finds the index of the minimum element.

When the current element is smaller than the current minimum, the program updates the index of the minimum. The program determines the minimum index and then swaps the current minimum with the current element within the outer loop. At last, we have the array in ascending order as an output.

void selection_sort(int arr[]) {
    int n = arr.length;

    
    //  Loop for each iteration
    for (int i = 0; i < n - 1; i++) {
      int min_idx = i;

       
       // Loop to find index of minimum element for ith index in each iteration
      for (int j = i + 1; j < n; j++) {

        // Check for the minimum element in each iteration.
        if (arr[j] < arr[min_idx]) {
          min_idx = j;
        }
      }

      // put that minimum element at ith index using temp variable
      int temp = arr[i];
      arr[i] = arr[min_idx];
      arr[min_idx] = temp;
    }
  }

3.2. Demo

Let us combine both functions and run the program to verify the output.

public static void main(String args[]) {

  int arr[] = {55, 29, 16, 23, 14};
  System.out.println("Original Array: " + Arrays.toString(arr));

  SelectionSort selectionSort = new SelectionSort();

  selectionSort.selection_sort(arr);
  System.out.println("\nSorted array: " + Arrays.toString(arr));
}

The program output:

Original Array: [55, 29, 16, 23, 14]

Sorted array: [14, 16, 23, 29, 55]

4. Time and Space Complexity of Selection Sort

4.1. Time Complexity

Selection sort has a time complexity of O(n^2), where n represents the size of the array. The algorithm involves two nested loops, each iterating n times. As a result, the total number of iterations equals n multiplied by n, equal to n^2.

In all cases(best, worst, average) the time complexity of the selection sort is O(n^2).

4.2. Space Complexity

Selection sort has a space complexity of O(1), indicating that the algorithm utilizes a constant amount of memory that is independent of the input size. The reason for this is that the selection sort operates on the input array directly, without generating any new data structures or utilizing additional memory for storing intermediate outcomes. Instead, it uses some temporary variables for executing swaps and comparisons, which necessitates constant space.

5. Advantages and Disadvantages

5.1. Advantages

1. Stability: Selection sort preserves the original order of equivalent elements within the input array. This feature is critical in certain use cases that necessitate maintaining the order of equal elements.
2. Space efficiency: Selection sort is an in-place sorting algorithm that can sort the data without requiring additional memory. This property makes it exceptionally efficient in terms of space complexity, particularly for large datasets with restricted memory resources.
3. Adaptability: Selection sort is easily adaptable to sorting an array in descending order or selecting the maximum value instead of the minimum value. This flexibility makes it a versatile algorithm suitable for various applications.
4. Simplicity: Selection sort is a straightforward algorithm that does not require any complicated data structures or recursion, making it simple to comprehend and utilize, even for beginners.

5.2 Disadvantages

1. Time complexity: The selection sort has a time complexity of O(n^2), resulting in rapid performance degradation as the size of the input array increases. This aspect is terrible for processing large datasets or arrays, where more sophisticated algorithms like merge sort or quicksort might be more suitable.
2. Inefficient for partially sorted arrays: Selection sort performs a fixed number of comparisons and swaps for each element, irrespective of whether the input array is partially sorted or not. This characteristic implies that selection sort may not be efficient for arrays that are already partially sorted or nearly sorted.
3. Low performance with repeated elements: The selection sort’s performance degrades when it encounters arrays with duplicate elements, resulting in unnecessary comparisons and swaps. This aspect can cause selection sort to be slower and less efficient than other sorting algorithms that handle repeated elements more effectively.

6. Conclusion

To summarize, selection sort is a space-efficient and uncomplicated sorting algorithm that operates by selecting the minimum value repeatedly in an unsorted portion of an array and swapping it with the first element of that portion. Although selection sort offers several benefits, such as its stability, space efficiency, and simplicity, it also has some drawbacks, including its time complexity, limited adaptability, and inefficiency when working with partially sorted arrays and duplicate elements.

A selection sort is suitable for processing small datasets or arrays, but it is not the optimal algorithm for larger datasets or arrays. Frequently, people combine it with other sorting algorithms to enhance performance and efficiency.

Happy Learning !!