Merge sort algorithm functions by partitioning the input array into smaller sub-arrays, sorting each sub-array recursively, and subsequently merging the sorted sub-arrays to generate the final sorted array. We reiterate this process until we sort the complete array.
This Java tutorial will provide an in-depth exploration of merge sort, its working, complexity, and its implementation in Java. Additionally, we will explore some of the key advantages and disadvantages of the merge sort.
1. How does Merge Sort Works?
Merge sort is an efficient sorting algorithm that utilizes the divide-and-conquer strategy to sort a list or an array of elements. It operates by repeatedly breaking down the input array into smaller sub-arrays until each subarray consists of a single element.
- In the beginning, we identify the midpoint of the array and split it into two subarrays of equal size.
- The next step involves recursively sorting the sub-arrays created in the previous step. We repeat this process until each sub-array contains only one element because we consider a sub-array of a single element to be sorted.
- After sorting the sub-arrays, we will merge the sub-arrays. This merging means comparing the elements of the two sub-arrays and arranging them in sorted order within a temporary array. We repeat this operation until we have placed all the elements in the temporary array.
- The temporary array contains the elements of the sorted array after the merge process is completed. The final step involves transferring these sorted elements from the temporary array back to the original array.
2. Merge Sort Example
Now, let’s move on to an example and understand how it works.
Let us take an array [10, 8, 9, 4, 3, 2], so suppose starting index (i.e 0) is “ l ” and the last index (i.e 5) is “ r ”. Here l and r mean left and right. Now below we will understand the above diagram step by step.
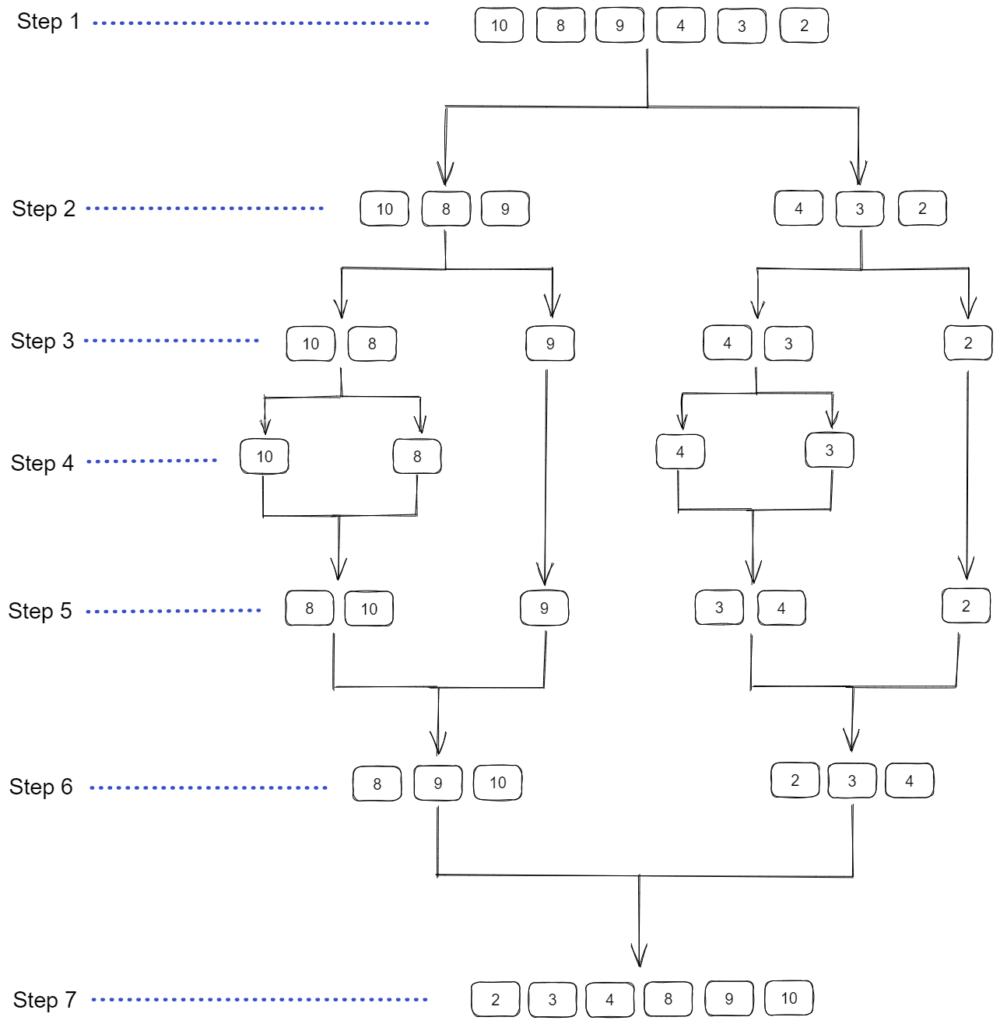
Step 1: In the given array let l=0 (starting index) and r=5 (last index). Now we have to divide an array into 2 equal parts by finding the middle index of an array.
Here, l = 0 and r = 5, so we calculate the middle index of an array as mid = (left + right) / 2.
So according to this formula, the middle index of the given array will be mid = 2, now we have got the index from where we have to break the array into 2 subarrays.
Step 2: Divide these 2 subarrays similarly using the formula, into 2 subarrays, one of size 2 and the other of size 1.
Step 3: As 9 and 2 are atomic elements in this step and we can’t further divide them into subarrays, we will divide the remaining elements.
Step 4: Since each subarray has only one value left, we cannot further divide them. Instead, we’ll consider every subarray as sorted.
Step 5: From here on, merge the elements in a sorted manner by comparing their values with each other. We merged 10 and 8 into a sorted array [8, 10] by comparing their values, and similarly merged 4 and 3.
Step 6: In this step, combine 9 with [8, 10] and 2 with [3, 4] in a sorted manner by comparing their values.
Step 7: Combine both arrays, [8, 9, 10] and [2, 3, 4] in a sorted manner by comparing their values. So at last we have got our sorted array.
3. Implementation of Merge Sort in Java
Let us hit the keyboard and write a program to demonstrate how to implement merge sort in Java.
3.1. Sort
Firstly create a function sort() which will take array (arr), starting index(l), and last index(r) as arguments and check there is more than 1 element in the array. If l<r then it divides the array into 2 sub-arrays from the middle using the formula (l + r) / 2, and then recursively calls the sort function for both the sub-arrays. And when we have both subarrays sorted then we will merge both of them in a sorted manner using the merge() function.
void sort(int arr[], int l, int r) {
if (l < r) {
int m = (l + r) / 2; // find middle index of an array
sort(arr, l, m); // sort left sub-array
sort(arr, m + 1, r); // sort right sub-array
merge(arr, l, m, r); // merge both sorted sub-arrays
}
}3.2. Merge
The merge() function takes an array, starting index, mid-index, and the last index of the array (r) as arguments. We then create two temporary arrays L and R of the same size as those subarrays. Now copy the elements of sub-arrays into L and R.
Now compare the first element of the left sub-array with the first element of the right sub-array. If the first element of the left subarray is less than or equal to the first element of the right sub-array, copy it to the resulting arr array and increment the index i.
Otherwise, the first element of the right subarray is copied to the arr array, and the index j is incremented. We repeat this process until we reach the end of either the left sub-array or the right sub-array. If any remaining elements exist in the left sub-array at this point then copy them to the arr array.
Similarly, If the right sub-array contains any remaining elements, the arr array copies them. By the end of this process, the arr array contains all the elements from both subarrays, sorted in ascending order.
void merge(int arr[], int l, int m, int r) {
// find out the sizes of the two subarrays that are going to be merged.
int n1 = m - l + 1;
int n2 = r - m;
// Create temporary arrays
int L[] = new int[n1];
int R[] = new int[n2];
// Copy all elements into temporary arrays
for (int i = 0; i < n1; ++i) {
L[i] = arr[l + i];
}
for (int j = 0; j < n2; ++j) {
R[j] = arr[m + 1 + j];
}
// Merge temporary arrays
int i = 0, j = 0; // starting indexes of array L and R
int k = l; // starting index of merged sub-arrays
while (i < n1 && j < n2) {
if (L[i] <= R[j]) {
arr[k] = L[i];
i++;
} else {
arr[k] = R[j];
j++;
}
k++;
}
// copy the elements which are remaining in L sub-array.
while (i < n1) {
arr[k] = L[i];
i++;
k++;
}
// copy the elements which are remaining in R sub-array.
while (j < n2) {
arr[k] = R[j];
j++;
k++;
}
}3.3. Demo
Let us combine both functions and run the program to verify the output.
public static void main(String args[]) {
int arr[] = {10, 8, 9, 4, 3, 2};
System.out.println("Original Array: " + Arrays.toString(arr));
MergeSort mergeSort = new MergeSort();
mergeSort.sort(arr, 0, arr.length - 1);
System.out.println("\nSorted array: " + Arrays.toString(arr));
}The program output:
Original Array: [10, 8, 9, 4, 3, 2]
Sorted array: [2, 3, 4, 8, 9, 10]4. Time and Space Complexity of Merge Sort
4.1. Time Complexity
Merge Sort is a recursive algorithm, and the following recurrence relation can be used to express its time complexity.
T(n) = 2T(n/2) + O (n) 2T(n/2) is for the time required to sort the sub-arrays, and O(n) is the time to merge the entire array. The answer to the above recurrence is O(n*Log n). An array of size N is divided into a maximum of Log n pieces, and the worst-case run time of this technique is O(N).
So O(n*log n) will be the time complexity in all 3 cases i.e worst, average, and best because merge sort splits the array in half and takes linear time to merge the two parts.
4.2. Space Complexity
To combine the sorted subarrays after sorting, temporary arrays are created in merge sort. These temporary arrays are used to store the sorting process’ intermediate results.
Merge sort has an O(n) space complexity, where n is the length of the input array. This is due to the fact that throughout the sorting process, merge sort generates temporary arrays of size n. As a result, the space needed by merge sort increases linearly as the input array gets longer.
Due to its O(n*log n) time complexity and comparatively low O(n) space complexity, merge sort is an effective and dependable sorting algorithm for huge datasets.
5. Advantages and Disadvantages
5.1. Advantages
- Guaranteed Time Complexity: The best comparison-based sorting algorithm currently used is merge sort, with a worst-case time complexity of O(n log n). This means that regardless of the initial order of the elements in the array, Merge Sort will always take the same amount of time to sort an input of size n.
- Low Space Complexity: Merge Sort consumes little additional memory to sort the input array because of its O(n) space complexity. This is helpful when sorting huge datasets that don’t fit in memory.
- Versatility: In addition to arrays, merge sort can also sort other types of data structures like trees and linked lists.
- Stable Sorting: As a stable sorting algorithm, merge sort keeps the relative order of equal elements in the output of the sorting process. This capability comes in handy for a variety of tasks, such as sorting a list of individuals first by first name and then by last name.
5.2. Disadvantages
- Recursive: Due to the expense of function calls, recursive algorithms may be slower than iterative algorithms.
- Not In-Place: When working with limited memory, Merge Sort can be a disadvantage because it needs extra memory to hold the temporary arrays used in the merging operation.
- Not Adaptive: The merge sort’s performance is not flexible because it does not use the input’s pre-sorted subarrays. This could lead to worse performance on partially sorted data when compared to other sorting algorithms like insertion sort.
6. Conclusion
Merge Sort is a reliable and stable sorting algorithm with a minimal space complexity of O(n) and a guaranteed time complexity of O(n*log n).
Merge sort is a popular choice for sorting huge datasets despite the fact that it is not an in-place sorting algorithm since its benefits outweigh its drawbacks. Merge Sort is a dependable and effective method for many computer science applications due to its stable sorting, adaptability, and versatility.
Happy Learning !!

Comments