The bubble sort algorithm functions by repeatedly comparing and swapping adjacent elements of an array until the complete array is sorted. The term “bubble” in its name refers to the way in which an element shifts in the array, resembling the movement of air bubbles in the water. As water bubbles ascend to the surface, the elements in the array move toward the end with each iteration.
This Java tutorial will provide an in-depth exploration of bubble sort, algorithm, complexity, and its implementation in Java. Additionally, we will explore some of the key advantages and disadvantages of the bubble sort.
1. Bubble Sort Algorithm
Bubble sort is a sorting algorithm that compares adjacent elements in an array repeatedly and swaps them if they are out of order.
Now, let’s understand the working of the Bubble sort Algorithm.
- Compare the first and second elements of the array starting from the first element.
- If the first element is greater than the second element, swap them.
- Keep moving to the next pair of adjacent elements and repeat step 1 until you reach the end of the array.
- Repeat steps 1 to 3 for the entire array until no more swaps are needed.
After the whole process, the array is sorted.
2. Bubble Sort In Action
Let us take an array [6, 2, 5, 3, 1]. It has unsorted numbers.

1st Iteration:
Starting with the first two elements, sorting will begin. To determine which is greater, let’s compare them.

Because 2 < 6, we need to perform a swap, and after completing the swap, the new array will look like this.

Now we will compare 6 and 5.

Because 5 < 6, we need to perform a swap, and after completing the swap, the new array will look like this.

Now we will compare 6 and 3.

Because 3 < 6, we need to perform a swap, and after completing the swap, the new array will look like this.

Now we will compare 6 and 1.

Because 1 is smaller than 6, we need to perform a swap. After completing the swap, we reach the end of the array. The resulting array after the first pass will be:

Now after the first pass, the largest unsorted element reached its correct position.
2nd Iteration:
During the second pass, the procedure will repeat itself. But this time it will not compare “6” with any other element since it is sorted.
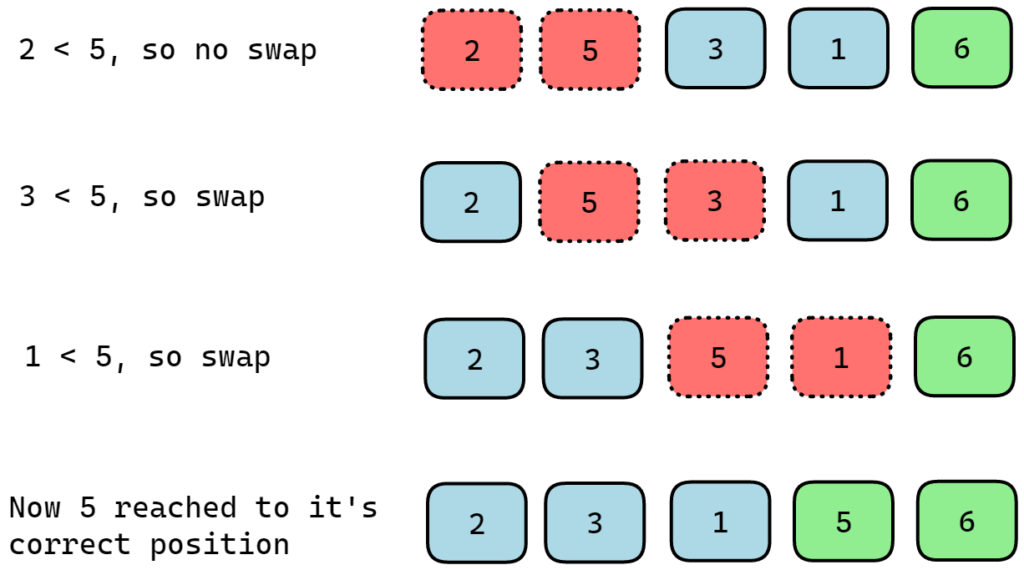
Now after the second pass, 5 reached its correct position.
3rd Iteration:
During the third pass, the procedure will repeat itself. But this time it will not compare “5 6” with other elements since they are sorted.
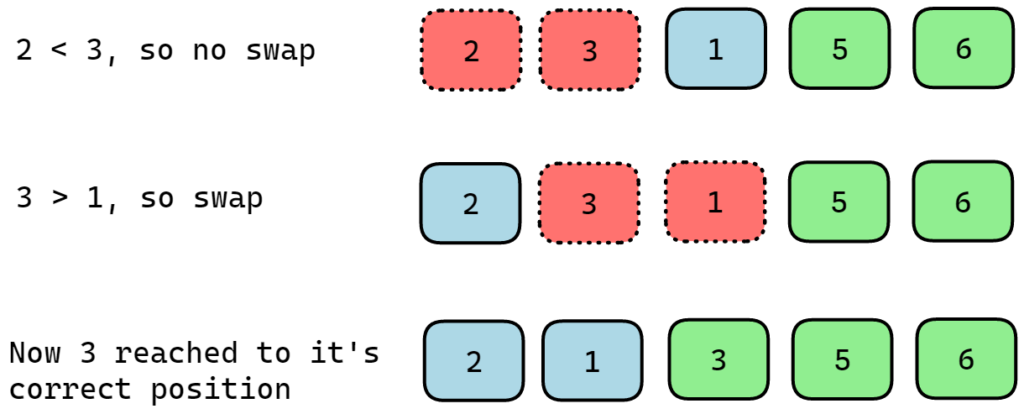
Now after the third pass, 3 reached its correct position.
4th Iteration:
During the fourth pass, the procedure will repeat itself. But this time it will not compare “3 5 6” with other elements since they are sorted.
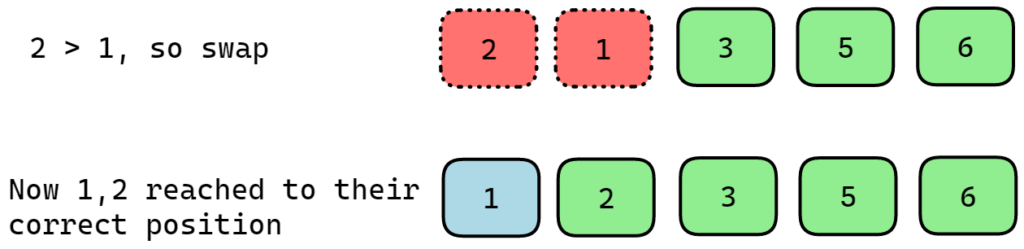
Now after the fourth pass, 1 and 2 reached their correct position. At this point, the array does not require any further sorting, so the final sorted array will look like this:

3. Implementation of Bubble Sort in Java
In bubble sort, we create two loops. The outer loop keeps track of the iterations and it starts from the first element and goes up to the second-to-last element in the array. The inner loop iterates over each element in the current iteration.
During each iteration of the inner loop, the algorithm compares the current element (indexed by “j”) with the next element (indexed by “j+1”). The algorithm swaps the current element with the next element if the current element is greater than the next element, using a temporary variable called “temp”.
Once the inner loop completes, the largest element in the unsorted portion of the array will be at the end of the array. At last, we will sort the input array “arr” in ascending order. Note that bubble_sort() function modifies the input array directly, rather than creating a new sorted array.
static void bubble_sort(int arr[]) {
int n = arr.length;
// Loop for each pass
for (int i = 0; i < n - 1; i++) {
// Loop to iterate over each element in each pass
for (int j = 0; j < n - i - 1; j++) {
// compare two adjacent elements, if swapping is required then do so
if (arr[j] > arr[j + 1]) {
// swap both elements using temp variable
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
}Let us use the sort function and run the program to verify the output.
public static void main(String args[]) {
int arr[] = {6, 2, 5, 3, 1};
System.out.println("Original Array: " + Arrays.toString(arr));
BubbleSort bubbleSort = new BubbleSort();
bubbleSort.bubble_sort(arr);
System.out.println("\nSorted array: " + Arrays.toString(arr));
}The program output:
Original Array: [6, 2, 5, 3, 1]
Sorted array: [1, 2, 3, 5, 6]4. Optimized Bubble Sort
Even if the array is already sorted, all comparisons are performed in the algorithm mentioned above, leading to an increase in execution time. Introducing an additional variable called “swapped” can address this issue. The algorithm assigns the value of “swapped” as true when it swaps elements. Otherwise, it assigns it as false when no swapping occurs after an iteration.
If the value of swapped remains false after an iteration, this implies that the elements are already sorted, and therefore, further iterations are unnecessary. This approach optimizes bubble sort by reducing the execution time.
Let’s have a view of the optimized bubble sort function.
static void optimized_bubble_sort(int arr[]) {
int n = arr.length;
// Loop for each pass
for (int i = 0; i < n - 1; i++) {
// variable for checking swapping
boolean swapped = false;
// Loop to iterate over each element in each pass
for (int j = 0; j < n - i - 1; j++) {
// compare two adjacent elements, if swapping is required then do so
if (arr[j] > arr[j + 1]) {
// swap both elements using temp variable
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
// set swapped to True to ensure that
// array still needs further iterations to be sorted
swapped = true;
}
}
// If swapped is still False after full iteration of pass
// it means array is fully sorted now, no further iterations are needed
if (!swapped) {
break;
}
}
}5. Time and Space Complexity
5.1. Time Complexity
Bubble sort uses an inner and outer loop, with the inner loop performing a deterministic O(n) number of comparisons.
- Worst Case: where the outer loop runs O(n) times, resulting in a time complexity of O(n^2).
- Best Case: where the array is already sorted, bubble sort still performs O(n) comparisons to verify the sorted order.
- Average Case: is O(n^2), which is a result of requiring (n/2) passes and O(n) comparisons for each pass on average.
4.2. Space Complexity
Bubble Sort does not require the creation of any new arrays or data structures, and recursion is not necessary. The algorithm only needs to maintain a few variables such as index values and a temporary variable to swap elements during the sorting process.
Therefore, the space complexity of Bubble Sort is O(1), meaning that the amount of extra memory used by the algorithm remains constant regardless of the input array size. This makes Bubble Sort an efficient sorting algorithm in terms of memory usage, especially compared to other algorithms like Merge Sort or Quick Sort, which need to allocate additional memory to store intermediate results during the sorting process.
5. Advantages and Disadvantages
5.1. Advantages
- Space efficiency: With a space complexity of O(1), Bubble Sort uses minimal additional memory, which makes it a memory-efficient algorithm.
- Stable: Being a stable sorting algorithm, Bubble Sort maintains the original order of equal elements within the input array.
- Adaptive: Bubble Sort is an adaptive algorithm that performs efficiently on partially sorted arrays. When the array is already sorted, the algorithm can terminate early, resulting in improved performance in such cases.
- Simplicity: Due to its simplicity and ease of implementation, Bubble Sort is an ideal algorithm for teaching basic sorting concepts to beginners.
5.2 Disadvantages
- Inappropriate for real-time applications: Bubble Sort is not a suitable choice for real-time applications that require quick and efficient sorting of data, as its time complexity can lead to significant delays in processing large datasets.
- Not efficient for partially sorted arrays: Bubble sort is inefficient for partially sorted arrays since it still needs to compare each pair of elements to guarantee that the array is entirely sorted.
- Not efficient for sorting large datasets: Bubble sort has a time complexity of O(n^2) in the worst case, making it a slow algorithm for sorting large datasets. This makes it unsuitable for use in applications where fast sorting is essential.
6. Conclusion
To summarize, bubble sort is a straightforward sorting algorithm that is easy to grasp and execute. Nonetheless, it comes with a few significant downsides, including its inability to handle large datasets efficiently and partially sorted arrays. Moreover, Bubble sort is not ideal for real-time applications where speed and memory efficiency are essential.
Although Bubble sort can be helpful in some cases, such as sorting small datasets or for educational purposes, there are usually better sorting algorithms available for most applications.
Happy Learning !!


Comments