Tail Recursion Vs Non-Tail Recursion

Two significant types of recursion are tail recursion and non-tail recursion in which tail recursion is better than non-tail recursion. In this post, we will learn about both recursion techniques with examples.

1. What Is Recursion?

Recursion is one of the algorithms in the divide-and-conquer strategy. In recursion, a function calls itself directly or indirectly with a slight change in the input parameters.

For example, in the given function, we are printing the numbers in decreasing order for a given input number,

public static void printNumbers(int n) {
	if (n == 0)
		return;
	else {
		System.out.print(n + " ");

		// Recursive Call
		printNumbers(--n);
	}
}

JVM uses stack memory at the low level to allocate stack frames for each recursive method call. If the recursion is uncontrolled or goes too much deeper, eventually memory will be full to allocate further stacks and it risks the StackOverFlowError error.

2. What is Tail Recursion?

In tail recursion, no other operation is needed after the successful execution of a recursive function call. The function directly returns the result of a recursive call without performing any operations on it.

Let us take a few examples to understand better.

2.1. Find the Factorial of a Number using Tail Recursion

Let’s try one example to find the factorial of a number using tail recursion.

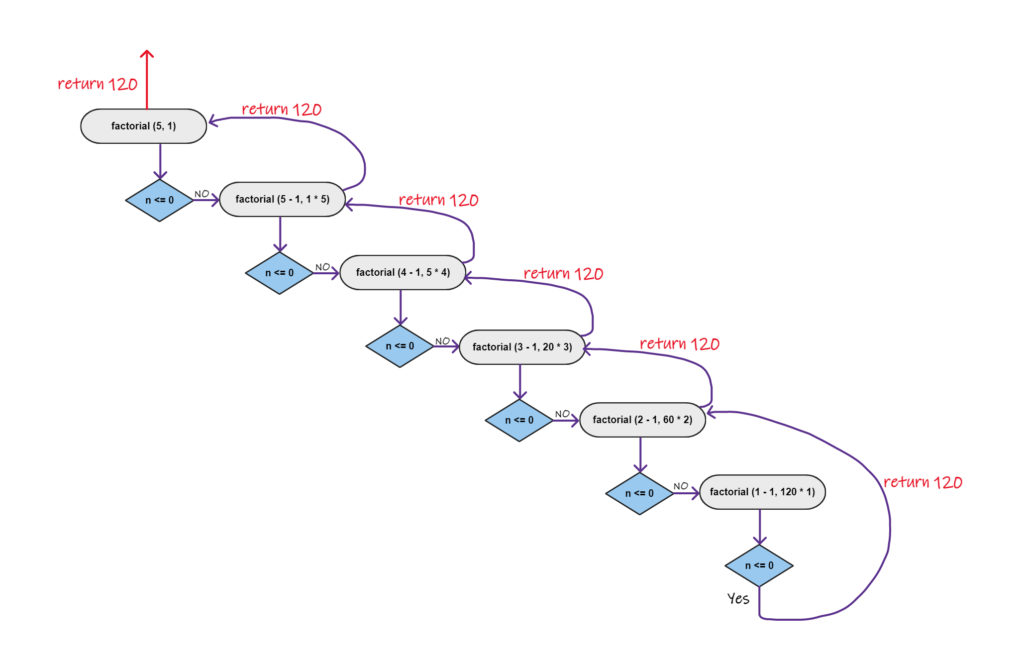
The following is the pseudo-code for calculating the factorial using tail recursion. Note that the return value of a recursive call is not utilized and simply returned from the function.

function factorial (currentNumber , previousMultiplication):
    if currentNumber is less or equal to 0 then
        return previousMultiplication
    else 
        return factorial( currentNumber - 1, currentNumber * previousMultiplication )
    end
end

We can visualize the whole recursive call flow with the following diagram.

2.2. Print First N Numbers in Fibonacci Series

Let’s try another example to print the first n numbers in the Fibonacci sequence using tail recursion. The following is the Java code that finds these numbers.

Note that the print() method does not return any value.

public class FibonacciSequence {

	public static void main(String[] args) {
		print(8, 0, 1);
	}


	public static void print(int n, int a, int b) {
		if (n > 2) {
			if (a == 0) {
				System.out.print(a + " ");
				System.out.print(b + " ");
			}
			System.out.print((a + b) + " ");
			print(--n, b, a + b);
		} else {
			System.out.println("size must be >2");
		}
	}
}

Program Output

0 1 1 2 3 5 8 13 

In both above examples, no operation is performed after the recursive call, or no operations are performed with the returned value by the recursive call. Hence both are Tail Recursive.

3. What is Non-Tail Recursion?

In non-tail recursion, some operations must be performed after successfully executing a recursive function. The function never directly returns the result of a recursive call. It performs some operations on the returned value of the recursive call to achieve the desired output.

Let’s try one example to find the factorial of a number using non-tail recursion.

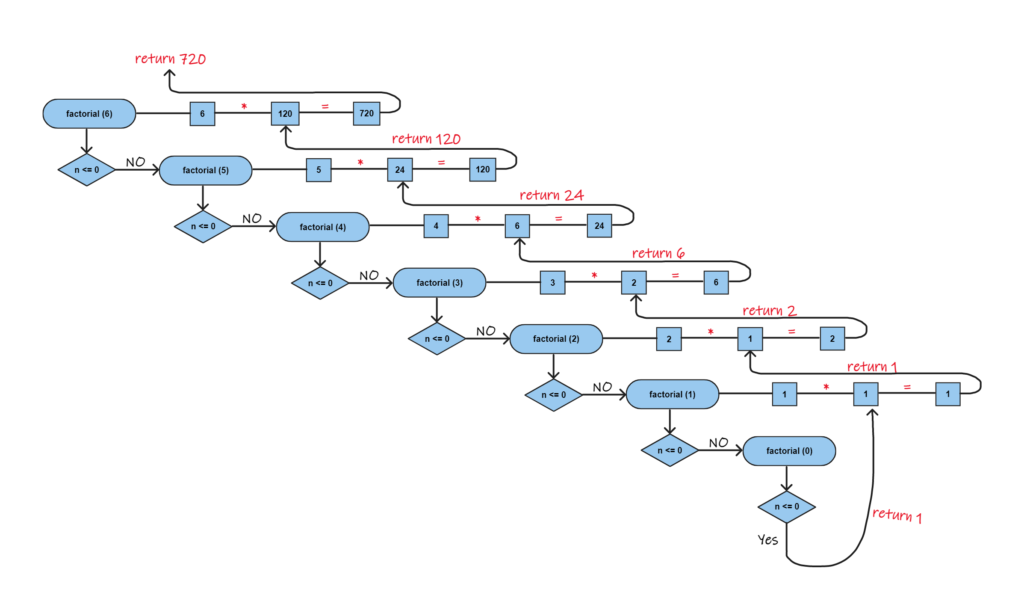
In the following pseudo-code, the value returned by factorial() recursive call is multiplied by the current number. It forces the JVM to retain the stack frames because the computed value will be multiplied by another value in future.

function factorial ( n ):
    if n is less or equal to 0 then
        return 1
    else
        return n * factorial ( n - 1 )
    end
end 

The following is the representation of finding the factorial using the non-tail recursion algorithm.

4. Which One is Better? Tail or Non-Tail Recursion?

Tail recursion is considered better than non-tail recursion because tail recursive functions can be optimized by modern compilers.

As we have seen above most programming languages use Stack Memory to store the order of method execution. This means when we make any recursive call then that call is pushed inside a Stack Frame.

In the case of tail recursion, modern compilers know that since it is tail recursive and no other operations will be performed after the recursive call, there is no need to maintain a stack. Thus retaining the current function call in the stack frame is of no use.

While non-tail recursion fully utilizes the stack frame and uses the value returned from the recursive call. JVM must retain all the stack frames, no matter how many they are, to compute the end result correctly. This leads to memory overuse and sometimes results in errors.

5. Can We Convert a Non-tail Recursion to a Tail Recursion? Always?

The answer is YES. We can convert any Non-tail recursive function to a Tail recursive function by passing additional parameters to maintain the state of the recursive call.

The idea is to maintain the result of calculation throughout the recursive calls, from start to end. Do not wait to compute the result until the terminal condition is met. Carry the intermediate calculation result along with a recursive call in each frame. Thus JVM does not need to maintain the old stack frames, thus saving memory.

We have seen both solutions for finding the factorial of a number in this tutorial.

static int factorial(int n) ;    //Non-tail recursion

static int factorial(int n, int previousMultiplication) ;   //Tail recursion

Sometimes, the conversion will not be easy and require additional changes. If non-tail recursion provides easy-to-read code and does not risk memory issues, we can stick with it to avoid unnecessary complexities in the code.

6. Conclusion

This tutorial taught us the basics of tail recursion and non-tail recursion. We also learned the main differences between both styles or recursions with examples.

Happy Learning !!

Sourcecode Download