Jump Search Algorithm

Jump search algorithm is used for searching an element in a sorted array. The jump search or block search searches an element into a sorted array by skipping/jumping ahead by a fixed number of elements in each step. In this way, jump search checks fewer elements than linear search.

Jump search algorithm performs better than linear search but not better than binary search, and this works only on sorted arrays.

1. How does Jump Search work?

In jump search, we traverse the sorted array and jump ahead with the specific block size. We will determine the block size to jump by getting the square root of the size of an array. i.e √n where n is the length of the sorted array.

When we find an element greater than the search element, a linear search is performed in the current block. The element, if present in the array, will be found in the block.

As jump search uses blocks in the search operations, it is also known as block search algorithm.

1.1. Algorithm Steps

Let’s understand the sequence in steps:

1. Sort the array if not sorted already.
2. Calculate block size to jump. Generally, it is the square root of array length.
3. Traverse the sorted array and jump elements based on calculated block size.
4. Perform linear search when the current value is greater than the given value.
5. Return the index of the element once a match is found.

1.2. Jump Search Example

Let us understand with an example. We have elements 10, 20, 30, 40, 50, 60, 70, 80, 90 and we are searching for element 60. In our example, the array is sorted so we can skip it.

Calculate the block size to jump i.e √9 = 3. So we will traverse the given sorted array and skip 3 elements each time.

At each step, we will compare the current element value with the search element. If the current element is less than the search element, continue jumping to the next block. If the current element is greater than the search element then perform a linear search from the previous step element to the current step element.

In our example, we started searching for element 60 from index 0 and jumped to index 3 and then to index 6. When we found that the current element at index 6 is 70 and it is greater than the current value of 60. So we start searching element from the previous index (3) to the current index (6).

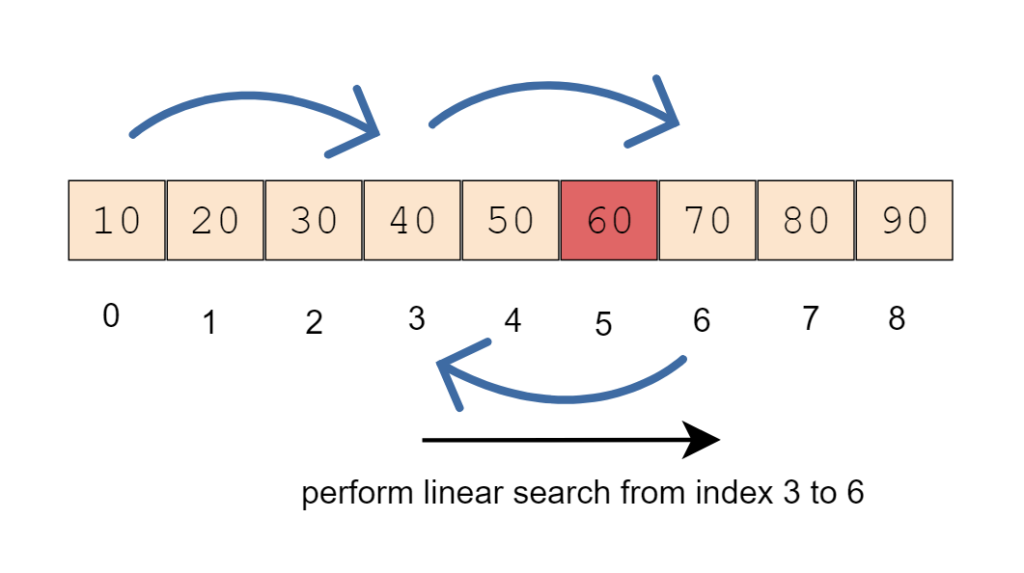
As soon as a match is found, we will return the index of the element.

2. Implementing Jump Search in Java

In the following example, we are:

• declaring and initializing the sorted array arr and search element ele.
• calculating the length of the array and assigning it to variable n.
• calculating the block/step size to jump and assigning it to variable step.
• defining the jumpSearch() function that accepts an array, search element, array length, and step as a parameter. It returns the index of the element if a match is found; else return -1.
• storing the previous step in variable prev.
• traversing the array till the current element is less than the given element.
• traversing the array using a linear search algorithm from the prev index element to the given element, we will return the index of the element if we find a match; else return -1.

public class JumpSearchAlgorithm {

  public static void main(String[] args) {
    int[] arr = {10, 20, 30, 40, 50, 60, 70, 80, 90};
    int ele = 60;

    int foundIndex = jumpSearch(arr, ele);
    System.out.println(foundIndex > 0 ? "Found at index : " + foundIndex : "Element Not Found");
  }

  public static int jumpSearch(int[] arr, int ele) {

    int prev = 0;
    int n = arr.length;
    int step = (int) Math.floor(Math.sqrt(n));

    //loop until current element is less than the given search element
    while (arr[Math.min(step, n) - 1] < ele) {
      prev = step;
      step += (int) Math.floor(Math.sqrt(n));
      if (prev >= n) return -1;
    }

    //perform linear search prev index element to given element
    while (arr[prev] < ele) {
      prev++;
      if (prev == Math.min(step, n)) return -1;
    }

    // Return index if element is found
    if (arr[prev] == ele) return prev;

    return -1;
  }
}

Found at index : 5

3. Time and Space Complexity

3.1 Time Complexity

The Jump search algorithm takes O(√n) time complexity.

3.2. Space Complexity

Since we are not creating any other temporary data structure, the jump search algorithm takes O(1) space complexity.

4. Conclusion

In this tutorial, we learned about the jump search algorithm and understood it with an example. This algorithm works only on sorted arrays and performs better than linear search but not greater than binary search.

Happy Learning !!

Source Code on Github